Selected Research Projects

Robustness for high dimensional statistical problems [Slides]

The past decade has seen successful extensions of M-estimation to the high dimensional setting with sparsity, e.g., using Lasso. Yet sparse modeling in high dimensions is NP-hard in the worst case. Thus theoretical sparse recovery guarantees for most computationally tractable approaches rely on strong assumptions on the probabilistic models of the data, such as sub-Gaussianity.

Meanwhile, statistical estimation with heavy tailed outliers or even arbitrary corruptions has long been a focus in robust statistics. But heavy-tails and arbitrary corruptions in the data violate the assumptions required for convergence of the usual algorithms. A central question then, is what assumptions are sufficient to enable efficient and robust algorithms for high dimensional M-estimation under heavy tails or arbitrary corruption.

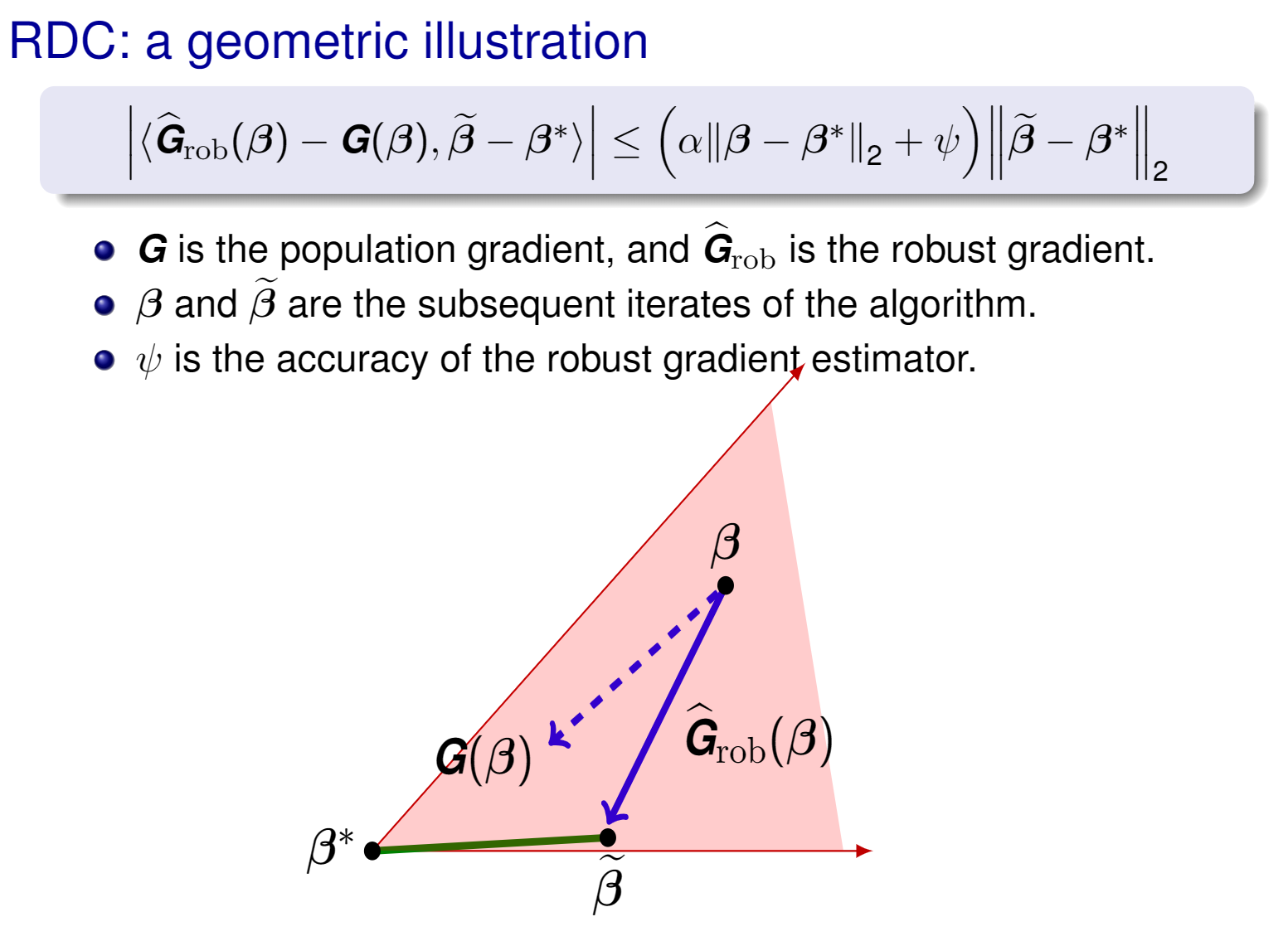
In this line of research, we define a natural condition we call the Robust Descent Condition (RDC), and show that if a robust gradient estimator satisfies the RDC, then Robust Hard Thresholding, is guaranteed to obtain good statistical rates. A key observation is the L2 norm requires bounds in all directions in high dimensions, yet hard thresholding operator guarantees that the trajectory goes through sparse vectors, we only need to bound a small number of directions for robust gradients. We show that this RDC is a flexible enough concept to recover known results, and obtain new robustness results. We also discuss estimating a low rank matrix in multitask learning with heavy tailed distributions.

For more detailed results in this project, please see our paper:
High Dimensional Robust M-Estimation: Arbitrary Corruption and Heavy Tails
Liu Liu, Tianyang Li, Constantine Caramanis.
ArXiv preprint arXiv:1901.08237, 2019. [Arxiv Link] [PDF] [Slides]